Have
you ever twirled a ball on a string? If not, try it. (It doesn't have
to be a ball, just something with several ounces of mass to it.)
Have
you ever twirled a ball on a string? If not, try it. (It doesn't have
to be a ball, just something with several ounces of mass to it.)You will feel a force; you have to pull on the string to make it work. The faster you twirl the ball, the more force you will exert on the string. And the heavier the ball, the more force you will exert on the string.
The phenomena at work here are called "centripetal force" and "centrifugal force". Here's what is going on.
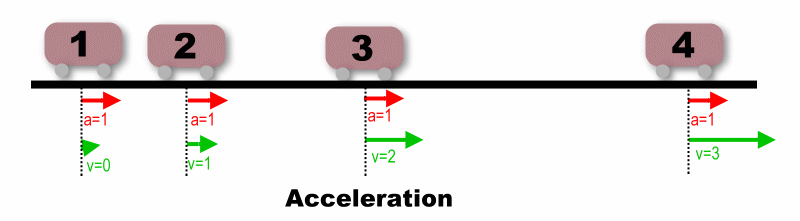
 Remember Newton? What would he say? In the absence of a force, the ball
would move in a straight line -- a constant velocity to the left. In
the picture, that is labeled
"Path without force". In order to make the ball move in a circle, we
need to exert a force
on the ball, in the direction of the
curvature we want to make in the ball's path. A force on a moving ball
at right angles to the direction the ball is moving has no component
either helping or opposing the existing velocity. So it will not change
the
speed of the ball, but it will change the direction. Remember, velocity
is a combination of speed and direction. In this case,
acceleration does change the velocity, but only the direction
component. It will put a curve on the ball's path. Such a
curve-producing force is called "centripetal force".
Remember Newton? What would he say? In the absence of a force, the ball
would move in a straight line -- a constant velocity to the left. In
the picture, that is labeled
"Path without force". In order to make the ball move in a circle, we
need to exert a force
on the ball, in the direction of the
curvature we want to make in the ball's path. A force on a moving ball
at right angles to the direction the ball is moving has no component
either helping or opposing the existing velocity. So it will not change
the
speed of the ball, but it will change the direction. Remember, velocity
is a combination of speed and direction. In this case,
acceleration does change the velocity, but only the direction
component. It will put a curve on the ball's path. Such a
curve-producing force is called "centripetal force".When we twirl a ball on a string, we are exerting a centripetal force on the ball through the string. Why do we feel a pull on the string? Let's turn to Newton again. He also pointed out that, for every force, there is an equal and opposite reaction force. So we are feeling the pull on the string in reaction to the centripetal force we put on the ball.
The reaction force to a centripetal force is called a "centrifugal force", and it is equal to the centripetal force and opposite in direction. Here are some properties of centripetal and centrifugal force:
- The faster you twirl the ball, the stronger the force.
- The heavier the ball, the stronger the force.
- The tighter the curvature you want, the stronger the force has to be. (A "tight curvature" means a smaller radius to the circle you're twirling.)
m v2Where:
F = ------
r
F = the centripetal or centrifugal force.There is some debate over whether centrifugal force is real. Indeed, some is and some isn't. But we aren't going to worry about it. For the limited purposes of explaining the motion of a golf club, we don't have to split hairs; the explanations and calculations work whether we treat the force as real or compute it as an acceleration. For the time being, it is the simplest way I know to explain the golf swing to a beginner -- at physics, not golf. There are other ways to explain it that are closer to the way a scientist would look at it, and I hope to do an article on that sometime. But it isn't here yet.
m = the mass of the moving body.
v = the velocity (really just the speed this time) of the moving body.
r = the radius of the circle you want the body to travel, called the "radius of curvature".