Physical principles -- energy 2

More energy

Angular energy

Just as we saw that torque was an angular analog of the linear quantity force, there is an angular energy that is an analog of the linear energy. Both work and kinetic energy in the angular domain are calculated as rather obvious analogs of their linear counterparts:

Work = Angular distance * Torque in the direction of that angle

Kinetic energy = ½ I ω²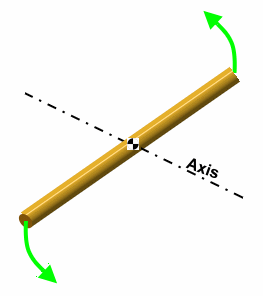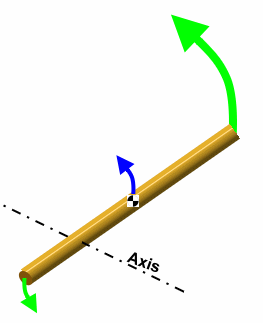

That isn't hard to understand in the diagram on the left, where the rotation is about the center of mass. No linear work is done, because the CoM never moves. Any moment of inertia involved is I_o, the inertia about the CoM. So the calculations are very straightforward.

Not so for the diagram on the right. This time, the axis of rotation is not through the CoM, so the CoM is going to move (its mothion is the blue arrow). There had to be an overall force to move the CoM. Remember the equivalent force couple systems? If you understand and remember what happened there, then you realize there has to be a net force in this diagram, because it is providing some linear acceleration to the CoM of the object.

Let's solve a problem like this that has a golf flavor. It might provide you some intuition about questions that come up in golf club fitting, though that process is much more complicated than this simple example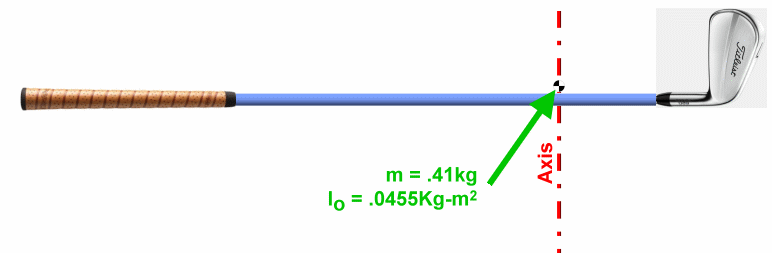

Here's our favorite seven-iron that we analyzed in previous chapters, and a few things we learned about it back then. Oh, that's right! The last time we were using the usual American clubmakers' units, inches and grams. Let's get used to solving problems in the MKS system that biomechanists will generally use. Here, we have simply converted the units:

Grams to kilograms.
Gram-inches-squared to kilogram-meters-squared.

The first conversion, g to Kg, is straightforward. If you had trouble with this one, you need to review the early section on measurement units. The other conversion is one you are not likely to find; even calc98 does not have the clubmakers' unit for moment of inertia. The way you convert g-in-squared to Kg-m-squared is:

Multiply the moment of inertia by the conversion from grams to Kg (1/1000).
Multiply that by the conversion from inches to meters (1/39.37).
Repeat step #2, because it has to be squared.

OK, let's move on to the problem:
How much work is done by a torque of 0.03 Newton-meters applied at the CoM for 2 seconds?
What is the kinetic energy of the club afterwards?

The solution
First, let's write down the basic stuff we know or can easily compute.

I = I_o = .0455 Kg-M²
T = αI so α = T/I = .03/.0455 = .66 rad/sec²

Now we know the angular acceleration, so we should be able to easily compute angular velocity ω and the angle traveled Θ. (You were told early on that you were expected to just know this, but I'll give you the link back to it if you forgot. Last time, though.)

ω = αt = .66 * 2 = 1.32 rad/sec

Θ = ½ α t² = ½ * .66 * 2² = 1.32 rad

... which happens to be an angle of 75.6 degrees.
Now we have everything we need in order to compute work and kinetic energy.

Work = ΘT = 1.32 * .03 = .0396 N-m

KE = ½ I ω² = ½ * .0455 * 1.32² = .0396 N-m

We have answer to the problem, but let's make an important observation. The work applied to the club is exactly equal to the kinetic energy it picked up. That is not a coincidence! One way even the most experience biomechanists check their work is to make sure (if the information is available) that the work done is equal to the useful energy created. (And, if they are not equal, where the rest of that energy went.)

Video clip courtesy of Steve Johnston PGA

Example: Waggle

Let's move on to a more interesting version of the same problem. Instead of applying to torque to the center of mass, we apply it where we normally would with our hands -- to the grip.The axis of rotation is now at the mid-hands point. But note, this is not a full swing, just a waggle as shown in the video. For purposes of this example, the major difference between this waggle and a full swing is that the hands, arms, and body never move; the only thing whose energy we care about here is the club itself.

Go ahead and try it yourself. Vigorously waggle a proper golf club back and forth, holding the mid-hands point still. No, not a shaft or dowel, a full club with plenty of mass and a CoM near the clubhead. You will find that, in addition to the torque (the hand couple) you must apply, you also have to apply a force to keep the hands in one place. The club wants to rotate around its CoM. If the CoM is far away from the hands, that means the handle end of the club wants to move opposite from the clubhead -- and it takes a force from your hands to prevent that motion. We will see this in more detail below.

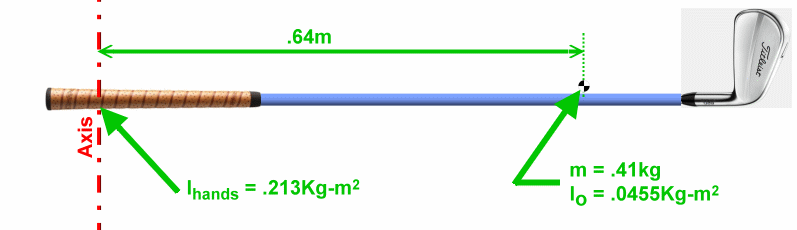Here is information we will need to solve the waggle problem, which we will state similarly to the problem we just solved.
How much work is done by a torque of 0.03 Newton-meters applied at the mid-hands point for 2 seconds? (Note that a force may be needed at the mid-hands point to assure that is the axis of rotation.)
What is the kinetic energy of the club afterwards?

This works very much like the previous problem, where the axis of rotation was the CoM. The numbers will be different, but the formulas are the same, as is the order in which we use them.

Again, let's start with the easy stuff. We need the parallel axis theorem to go from I_o (at the CoM) to I (at the mid-hands point).

I = I_o + mr² = .0455 + .41*.64² = .213
T = αI so α = T/I = .03/.213 = .141 rad/sec²

Now we know the angular acceleration, so we should be able to easily compute angular velocity ω and the angle traveled Θ.

ω = αt = .141 * 2 = .282 rad/sec

Θ = ½ α t² = ½ * .141 * 2² = .282 rad

... which happens to be an angle of 16.2 degrees.
Now we have everything we need in order to compute work and kinetic energy.

Work = ΘT = .282 * .03 = .0085 N-m

KE = ½ I ω² = ½ * .213 * .282² = .0085 N-m

Again, the work done by the hands on the club equals the kinetic energy of the club. Or does it?!? We have a couple of linear things to worry about here.

There is a force at the hands. Is it doing work? Well, no, it isn't doing work. It is applied at the axis, which does not move. Without motion in the direction of the force, the force does no work? So we're OK here.
The CoM of the club finishes with some linear motion. Isn't that kinetic energy? Actually, it is. We've miscomputed the kinetic energy by (a) ignoring this linear KE, and (b) using a moment of inertia other than I_o for the energy computation. Let's go back and do that KE calculation strictly rather than the loosey-goosey way we just did it.

Angular KE = ½ I_o ω² = ½ * .0455 * .282² = .0018 N-m
Linear KE = ½ m v²
And we know that, for a spot on a rotating body a distance r from the axis

v = rω = .64 * .282 = .18 m/s so
Linear KE = ½ m v² = ½ * .41 * .18² = .0066 N-m

Finally

Total KE = Angular KE + Linear KE = .0018 + .0066 = .0084 N-m

Yes, it comes out the same. (There is a round-off problem in the last digit, but that is all that is wrong.) It took me less than 20 minutes to prove that they will always come out the same, no matter where on the club you place the axis. But I won't bore you with the proof.

Other forms of energy

So far, we have talked about work, potential energy, and kinetic energy. Let's look at the other forms of energy we are taught in Physics 101. We'll review them quickly, because they are mostly irrelevant to the study of the golf swing. We'll note where there might be some relevance, and explain it.

Heat

When I think of heat energy, the first thing that comes to my engineering-trained mind is the sort of heat engine that has been the world's most important source of energy for the last century or two. I'm talking here about steam engines, internal combustion engines, and turbines. They power our transportation, and indirectly almost everything else we use. The vast majority of our electric power comes from generators turned by heat engines. All of them have heat as input, and some useful energy as output.

But the importance of heat energy in golf is quite the opposite. The heat is output, not input. It is the form of wasted energy, the unusable energy in the golf swing -- and almost all other enterprises that use energy. Let's stop for a moment and define efficiency, because inefficient use of energy is exactly where that heat comes from. Efficiency is:

Efficiency η =

Energy_out

Energy_in

For example, it you only get out half the energy you put in, the efficiency is 50%. (In golf and most technologies, there are other metrics that they call "efficiency". For instance, I have seen clubhead speed divided by the maximum possible clubhead speed called "speed efficiency" of a swing. But, strictly speaking, efficiency really refers to the useful energy you get divided by the total energy you supply.)

But we know that energy is conserved; it can not be created nor destroyed. So the missing energy has to go somewhere. And it almost always manifests itself as heat energy; something in the system gets a little warmer, heated by this "lost" energy.

Friction

In golf analysis, the lost energy is always heat, and usually due to friction. We know that friction can supply heat; think about starting a fire by rubbing sticks together. Maybe it doesn't supply a lot of heat; it takes a lot of effort to start a fire that way. But have you ever gotten a rope burn, when a rope you are holding "runs away" in your grasp. There's a pretty dramatic example of friction work turning into heat energy.

So how does friction work? At a "hand waving" level, something sliding across another surface is acted on by a force that resists its sliding. But let's be a little more precise.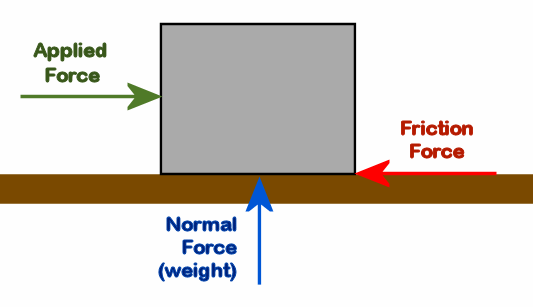

The diagram shows a block resting on the floor.

A force (green) is applied to the block, trying to make it slide on the floor.
Does it slide right away? No. The force has to get to some level before it overcomes the friction force (red) that resists sliding.
And how big is that friction force? It depends on the normal (which means perpendicular) force (blue), which in this example is just the weight of the block. Specifically, the maximum value the friction force can take is the normal force times a number called the "coefficient of friction" (usually designated "μ")

We all have enough experience to know that μ depends on the material. Ice is more slippery (lower friction) than sandpaper. In fact, the coefficient of friction depends on both materials that are touching. And it can have a big range from one material combination to another. For instance, steel on ice has μ=0.03; it doesn't take much applied force to get ice skates sliding across the rink. At the other end of the scale, μ can be greater than 1. That means if the surface is rough enough or "grippy" enough, the friction force might be more than the normal force. Here's a link to a table of coefficients of friction for a pretty wide variety of materials.

Just in case it isn't clear yet, here's how it works. In the following, A is the applied force, F is the friction force, and N is the normal force.

If A<μN, then the friction force F is equal to A and the block does not move.
If A>μN, then the friction force F=μN and the block slides. Any excess force A-F (which is a net force) accelerates the block as it slides.

One thing that should strike you is that work is being done in the second case! (In the first case, there is no motion so no work.) If the block slides a distance x across the floor:

The total work done to the block is xA, the force applied to the block times the distance the block moved. Simple so far.
The work done accelerating the block, x(A-F), turns into kinetic energy. So we have accounted for where that energy went.
But what about the work done against friction, xF? It doesn't turn into kinetic energy; it was just enough force to overcome friction, not to accelerate the block -- that is, add to the block's velocity. It doesn't turn into potential energy either; the floor is flat, so no height is gained. The only place that work can go is to turn into heat. Unless you have some sort of heat engine working from the temperature of the block or the floor, that work is lost. Not destroyed; it is still energy. But we can't do anything useful with it. That is the nature of friction forces; their work is usually just loss of useful energy.

Let's look at some examples of friction in golf:

Non-sliding friction force: This is the case where A<μN, so the surfaces stay locked together -- no sliding. There is a very important application of this in golf, the interface between the grip of the club and the hand or glove of the golfer. Designers of grips and gloves try to maximize the coefficient of friction, within the rules, so that the golfer can control the club slip-free with a minimum of grip pressure (normal force).
Sliding friction: There are not many places in the golf swing to point to for examples of sliding friction. And that stands to reason; we want the swing to be as efficient as possible. Any work we do in the swing we would like to turn into kinetic energy -- clubhead speed. But let's look at something we don't want to happen, but sometimes does. I'm talking about the fat hit. When the clubhead scuffs the ground on the way to the ball, the result is friction. The harder the club touches the ground, the more force. The farther the club drags on the ground (i.e.- the earlier it hits the ground), the more distance that force is acting on it. So we have a force decelerating the club for a distance, the definition of work. That work can be equated to a difference in kinetic energy of the clubhead at impact, a quantifiable loss of clubhead speed.
Static friction: If you looked closely at the table of coefficients of friction, you noticed that there are two columns for μ. labeled "static" and "kinematic (sliding)". That is because it usually takes a little more applied force to break the object free and get it started sliding than it does to keep it sliding. So there is a coefficient of static friction and a usually smaller coefficient of sliding friction. In many cases they are nearly the same, but some may show a big difference. For instance, clean and dry cast iron on cast iron has a static μ of more than 1, but once it is sliding the μ is only 0.15.
Rolling friction: when something round rolls across a surface ,there is some friction. True, it is usually a lot less friction than if it were sliding, but there is almost always some measurable friction. Ball bearings are used to reduce force, because surfaces are no longer sliding, but that force is reduced, not completely eliminated.

How about a golf example of rolling friction? Do you know what "stimp" is? No, really, do you know what stimp is? It is a measure of the friction between a green and a ball rolling on it. The less the friction, the higher the stimp number. Here is an article I wrote about an interesting bet, where its payoff depends on rolling friction. Section 1 is almost a textbook example for our discussion of rolling friction, potential energy, and kinetic energy.

Internal friction: Friction and its associated energy dissipation can show up even without visible surface-to-surface contact. For instance, the golf ball is compressed on the clubface during impact. It doesn't look like there is any sliding between clubface and ball, and in fact there is very little. But internally, within the golf ball, the particles making up the layers of the ball are rubbing together, with resulting frictional losses. This does not follow any of our formulas for dealing with friction, so another name has been associated with it: coefficient of restitution, or COR. Physicists and engineers usually designate it as e in equations.

As with friction, the restitution losses are associated with two different surfaces. Unlike friction, there are lots of interesting cases where the form is at least as important as the material. Our example of a golf ball compressing on the clubface is a classic in this regard. The clubface is titanium and the ball is usually a composite of natural and artificial rubbers. But the thickness of the face can account for a large proportion of the difference between the actual COR and 1.0 (which is a lossless collision). And that is true even though almost all the losses are in the ball, not the clubface. It is the combination that determines the COR.

Chemical

A small corner of chemical energy is at the core of biomechanics. The body burns nutrients to power the muscles. Our entire body is maintained by such chemical energy. However, it isn't part of the physics of the golf swing, and this tutorial is going to ignore it. Nutritionists and exercise scientists get deeply involved in chemical energy and the processes related to it. If you go on to do college degree work in biomechanics, I'm sure you will get plenty of exposure to this branch of the science. For our purposes, we are going to view muscles as engineers would; they are actuators with specifications and limitations. We'll get into that in the next chapter.

Electromagnetic

Electromagnetic energy is a very important practical branch of the study of physics and engineering. It includes:

Electric motors and actuators, to produce forces and motion.
Electromagnetic fields and waves, to allow wireless communication to and from devices.
Light (which is really just high-frequency electromagnetic waves), including solar power.

While all of these can play an important part in golf instrumentation and experiments, they have little or nothing to do with how the body swings a club. We are not going to mention it any further in these notes.

Nuclear

We do not have to worry about nuclear energy nor quantum mechanics in golf physics. Period! If anyone tells you otherwise, they need to have their heads examined -- or at least get a clue about physics. I only mention this because an otherwise knowledgeable golf expert once insisted to me that quantum effects are important in putting. Actually they were expert in tournament golf, not golf phsyics -- and it showed.

Last modified -- Dec 3, 2022

Physical principles for the golf swing

Energy and Momentum