|
| Home ⇒ golf ⇒ swing ⇒ Current Article |
Article
Contents
Accelerating Through Impact: Mandate or Myth
Dave Tutelman
-- January 7, 2012
|
 If we are going to
seriously consider the question, we have to state
the premise less vaguely. We are going to compare:
Note that I did not ask, "Is case 2 faster?" I asked for numbers. Numbers matter! If it is only a fraction of a mile-per-hour faster then, for all practical purposes, there is no difference. It makes no sense to say, "You get more distance by accelerating through the ball," if that extra distance is so small you can't even measure it reliably. However, if it is several miles-per-hour faster, that is a distance gain worth seeking. (Brief digression on this point. Much of my writing on this site is aimed at custom clubfitters and clubmakers. I have seen so many clubmakers spend a lot of time optimizing one parameter while ignoring or giving short shrift to a different parameter -- one that matters a lot more. Why? Because they know how to measure and adjust -- sometimes with great precision -- the one they spend time on. Old proverb: "When all you have is a hammer, you tend to treat everything as a nail." This article is about instruction, not clubmaking, but we are investigating a similar phenomenon -- focusing on something that makes a tiny difference, perhaps at the expense of something else that is important.) |
|
|
Simplified analysis #2 - Clubhead speedLet's try another way of looking at it. What would the clubhead speed be immediately after impact, if the clubhead had not lost any momentum from impacting the ball? Why would this matter? If the ball were not there, we have a speed before impact and another one 0.4msec after impact (i.e.- after separation). The clubhead speed that would be applied to the ball is somewhere between these two. So let's find both. Case 1: The clubhead speed coming into impact is 100mph. That is one of our original assumptions. Since Case 1 is the case of zero acceleration, the speed 0.4msec later is still 100mph. Case 2: Again, by assumption, the clubhead speed coming into impact is 100mph. We have an acceleration of 500 ft/s/s. Therefore, in the duration of impact, the change of velocity is given by the acceleration times the time the acceleration is happening: Change of velocity = 0.0004sec * 500 ft/s/s = 0.2 ft/sec = 0.14 mph Velocity 0.4msec after impact = 100 + 0.14 = 100.14mph. So, out of a clubhead speed of 100mph, the acceleration gives us a boost of only 0.14mph. That's only than a 0.14% gain, and represents an extra 15 inches of distance on the drive. Note that it is the upper bound of the gain in ball speed that you could expect; the actual distance gain will be less. It is even less than Simplified Analysis #1; this one is probably negligible even for a long drive competitor. (Not zero, true. But negligible.) |
Bottom Line
Our two back-of-the-envelope calculations show distance gains of no more than 4 feet and 1.3 feet respectively, and probably less than that. That's feet, not yards. In the appendix, I have a more detailed analysis that comes closer to an exact answer -- and it is even lower than the two simplified analyses. It only shows 8 inches of additional distance.For comparison, let's look at just a few other things you might be working on instead of accelerating the clubhead:
- Improve your wrist flexibility. Just one degree more of wrist cock is worth a yard and a half of extra distance. (No, not a lot. But almost seven times what clubhead acceleration is worth.)
- Get contact on the sweet spot. With most drivers, missing the sweet spot a half-inch low on the face will cost ten yards. (From my article on gear effect, and the HotStix data cited.)
- Work on your core strength.
An improvement of just 2% in the strength of your body rotation is
worth two and a half yards.
Which brings us to our second question...
Is it good instruction?
We just found that it makes no sense to say, "You get more distance by accelerating the clubhead through the ball," if that extra distance is so small you can't even measure it reliably. So why even mention it in instruction? Actually, I am in favor of teaching accelerating through the ball. But not because clubhead acceleration at impact will hit the ball farther. There are quite a few things that are bad physics but good instruction, and this is one of them. Let's look at some reasons that accelerating through impact is a good swing key.WHAT IS REALLY ACCELERATING?
Is it the clubhead, as is usually assumed by teachers telling us to "accelerate through impact"? If not, is it the hands? The body? Let's look at the possibilities.| Clubhead: |
 We've
already debunked the notion that you get more ball speed from an
accelerating clubhead. But there's another reason not to try to
accelerate the clubhead -- at least not unless you are doing it right.
The act of trying to add clubhead acceleration may itself be deleterious to
clubhead speed, if you do it in the obvious way. That seems like a non
sequitur -- it doesn't follow. But let's review where clubhead
acceleration can come from. We're doing physics here.The picture at the right shows the two ways the clubhead can still be accelerating at impact. One is good and the other not so good. Let's start out with the not-so-good one, the upper example. The wrists can be applying a torque to the handle, creating an accelerating force on the clubhead. The shaft must bend backwards to transmit the force. The reasoning is presented in my article on the right-hand hit. Most of that same article examines whether this sort of acceleration provides more clubhead speed or less. The conclusion is that, if applied with exquisite timing, strength, and hand speed, it might give a tiny bit more clubhead speed. But miss out on the timing, strength, or hand speed and it will cost far more distance than could possibly be gained by perfect application. So you don't want to accelerate the clubhead directly -- by forcing it with the hands and wrists. The lower example is a more productive way to apply clubhead acceleration through impact. The picture (which I adapted from Andrew Rice's web site) shows the proper position at impact for an iron shot, as exemplified by an impact bag drill. You want the hands leading the clubhead. This implies that the wrist cock is not completely released at impact; the green angle (which I added to Andrew's photo) shows the wrist angle at impact. If you understand how centrifugal release works ("inertial release", if you're going to be a stickler about terminology), you will recognize that this position has the clubhead still accelerating; the inertial release has not yet completed. I said this is more productive than accelerating the clubhead with wrist and hands. But why? There are a number of reasons.
|
| Body: |
The body turn involves angular
velocity and acceleration, so "accelerate through impact" might refer
to body rotation. In this category, I will lump together legs, hips,
trunk -- all the way up to the shoulders. That's because all have to be
involved to move the shoulders. The muscles of every link in that chain
must either create motion or trasmit it, up from the ground to the
shoulders. What happens if the body does not accelerate through impact? Well, once the ball is gone, anything that happens makes no difference. So, theoretically, acceleration beyond impact is not going to matter. But that's theory, and someone once pointed out to me, "The difference between theory and practice is bigger in practice than in theory." The problem with this theory is the difference between intent (or even "feel") and what the body is actually doing. This relates very directly to accelerating the body turn through impact. A real live human being cannot accelerate the body to impact and not still be accelerating through impact. A golfer thinking only of accelerating to impact is going to quit accelerating before getting near impact. You can't turn off full-body acceleration in .4 milliseconds, probably not even in 100 milliseconds.  In fact, a good instructor will have the golfer exaggerate... Accelerate well beyond impact. If you have taken a lesson where your swing was video'd, and watched the video afterwards, you know this is true. You may intend to make a particular exaggerated move, you may have felt that you made the move successfully, but it is barely there (if at all) on the video. Much of good golf instruction is getting people to greatly exaggerate a correct move, because it is the only way to get the motion to happen at all. So, assuming we want angular body acceleration to continue up to impact, the swing key to be taught is to accelerate well beyond impact. |
| Hands
and Arms: |
I subscribe to golf instruction
that says that the hands are moved by the body. But that is not the
only theory of instruction out there; I have read books that say things
like, "The arms do the swinging part of the golf swing... The body does
not swing. It reacts to the swing." I may disagree with that, but it might be a productive intent and feel for some golfers.
And that makes it valid instruction for those golfers. But -- make no mistake about this -- physics says that hand and arm motion is caused by body rotation. That is actual, as opposed to intent and feel. So, if we are going to analyze the physics of the swing, the motion of the hands and arms is driven by the body rotation. For the first approximation, we do not have to analyze hands and arms separately, just the body rotation -- which we discussed above. (If we were to refine the analysis, which I won't here, we would next account for the left arm's separation from the body late in the downswing. Still nowhere near "arms motivating the swing", but at least there may be some change of the result due to the rotation of the arm not being exactly the same as the rotation of the body.) |
CONSEQUENCES OF ANGULAR DECELERATION
Above we discussed the angular acceleration of the body. The argument above maintains that, unless you try to accelerate the body's rotation well through impact, you will in fact lose acceleration well before impact. In golf terminology, you will "quit on the shot." This has a number of consequences:- Distance
actually is lost. This has nothing to do with the clubhead
accelerating through the ball, but rather that less acceleration is
applied to the clubhead for tens of milliseconds before
impact. The clubhead is deprived of some of the accleration it would
have had, in order to build up speed at impact. And clubhead speed at impact is what really matters for distance.
- The left wrist is cupped, rather than the proper flat or even bowed left wrist. We know that a bowed wrist at impact (or a flat wrist at the very least) is desirable for a solid hit. A cupped wrist, on the other hand, is associated with lost clubhead speed, fat or thin shots, or too-high balloon shots. It is also likely to point the clubface to the left, resulting in a pull or even a pull-hook. (Think about it this way: if the swing plane were perfectly vertical, then a cupped left wrist would add loft. Since the swing plane is not vertical but tilted, some of that "loft" turns into a left-facing angle.)
| The
model: Torque variation during downswing |
Clubhead
speed at impact |
Wrist
angle at impact |
Constant accelerating torque
through
the downswing, no "quit".
|
107 mph |
3º bowed |
Our best approximation to the
classic "quit" scenario:
|
99 mph |
6º cupped |
Suppose, even with "quit", we
apply the same total torque-times-milliseconds to the swing as we did
earlier to the constant-torque swing. Real
swings don't work like that, but let's see how much of the effect is
due to the total torque-seconds applied and how much to the fact that
some
torque is withdrawn late.
|
104 mph |
6º cupped |
This table confirms the consequences we guessed at above:
- If you deprive the downswing of body torque by quitting on it, you lose clubhead speed -- and, obviously, distance. Not only that: the torque late in the downswing (the torque you lose when you quit) is more important than torque early in the downswing. How do we know? Because we still lost 3mph of clubhead speed (about 9 yards) in the third calculation, where the total torque-seconds were the same as the no-quit swing; the torque was larger early in the downswing and reduced during the "quit" at the end.
- Loss of body torque late in the downswing will indeed turn a bowed wrist (good!) into a cupped wrist (bad!).
- The first animation maintains body torque through impact -- that is, it keeps accelerating the body rotation through impact. The clubhead starts with a lot of lag, and really gets moving (develops a lot of momentum) late in the downswing. The clubhead has just about caught up with the hands as it impacts the ball, giving a flat or slightly bowed wrist position at this position.
- The second animation starts out the same, and maintains
acceleration for the first 200msec of the downswing. Then it gets
seriously torque-deprived. That is what we mean by "quitting on the
swing"; we don't apply energetic body turn through the ball. Because
we're only human, the loss of acceleration takes effect before we get
to the ball -- earlier than the quitter intended. You can see that the
hands (the red dots) are slowing down late in the sequence; the red
dots are closer together, so we know they are getting slower.
Meanwhile, the clubhead (the gray dots) has attained quite a bit of
momentum, even after just 200msec. True, not as much as if we had
continued to accelerate the rotation, but enough to catch and pass the
hands as they slow down. At this point, it's just geometry. The last
tens of milliseconds before impact, the slowing hands and not-slowing
clubhead result in a cupped wrist -- and all the evils that the cupped
wrist brings.
SHORT GAME IMPLICATIONS
So far, we have been talking about a full swing. But there are two pretty obvious implications for the short game as well. I haven't worked the numbers on this, but logic and plenty of anecdotal evidence seems to confirm it.- Putting
- In putting, the body turn becomes shoulder rock; the swing plane is
close to vertical. If you don't continue the shoulder rock well past
impact, your wrist will cup. That tends to cause a pull. People who are
"wristy" putters have learned to time the release to compensate for it.
But it is hard to teach, and a low-percentage high-maintenance stroke. Now that we know this little gem of information, putting
instruction has adopted a back-and-through motion with as steady a left
wrist as possible.
- Chipping
and pitching
- For these shots, wrist cock is negligible to nonexistent, so
centrifugal acceleration isn't going to be a factor. What is left is F=ma;
accelerating the clubhead through impact means that the hands, through
the shaft, are applying a force to the clubhead. With a clean strike,
the accelerating clubhead doesn't matter. But a slightly fat hit will
take more than 50% off the distance of a chip or pitch, as opposed to
maybe 10% or 20% from a full swing. That is because the clubhead is not
just transferring momentum to the ball; it is losing momentum to the
ground before it even gets to the ball. When the clubhead strikes a
ball, the only resistance is inertia. But the ground is adhered to the
earth, and the earth is for all practical purposes an infinite mass. So the club has to
administer enough force to cut some turf away from the earth. This is a
lot more force than just moving a free-sitting golf ball. So a lot of
the clubhead's momentum is lost providing the force needed to cut the turf.
What does this have to do with the accelerating force? Well, force applied to the clubhead can restore some of the lost momentum due to the fat hit. If it is seriously fat, then not much will be restored. But those slightly fat chips will get closer to where you want them if you are accelerating the clubhead all the way through the ball.
Still, like putting or even the full swing, you don't want the hands to create the acceleration, just transmit it from the shoulders. "Wristy" chips and even pitches are lower-percentage shots. Unless they are perfectly timed, the usual problems of a cupped wrist are likely to occur: fat hits and sculls. (Think in terms of Steve Stricker's motion; he is one of the most reliable wedge players in golf. He sets the wrist angle, then uses his hands, wrists, and forearms to keep the angle. The acceleration for the swing comes from the shoulders, and continues well through the ball.)
BOTTOM LINE
"Accelerate though the ball" is an excellent swing key, for every shot from a drive to a putt.But it is better expressed as "rotate your body through the ball" (or perhaps "accelerate moving your hands beyond the ball"), because it is body rotation or "turning the triangle" where acceleration through the ball is beneficial. Consciously accelerating the clubhead through the ball (especially if you do it with the hands, wrists, or forearms) will probably do more harm than good.
Acknowledgements
First off, I'd like to thank Jim McLean for asking the questions that sharpened the physics issue, to the point that there was something worth writing.Then Bob Corbo of Simductive Golf got on my case about wrist position and acceleration at impact. He insisted that he and all his students had much more solid ball-striking and never an over-the-top if the wrist is flat or bowed from the transition through well past impact. He challenged me to explain why. It was clear it had something to do with acceleration.
Appendix - More exact analysis
Here is a more detailed analysis of the physics of impact. We are going to look at the equations for momentum transfer from clubhead to ball, and see how that is affected by an accelerating clubhead. If you're not into the math and physics of it, you can skip the details below. Here's a peek at the ending: The distance gain you can expect from an accelerating clubhead is less than a foot -- only 8 inches.As in the simplified analyses, we will compare:
These two cases will be compared, to test the value of clubhead acceleration in creating ball speed.
We'll start with notation. The computation will be done using MKS units (meter-kilogram-second), to be sure we aren't making mistakes in units. We will convert back to the units we recognize (like pounds, miles per hour, etc) when we want to get a feel for what's going on.
- U denotes a velocity just before impact.
- V denotes a velocity just after impact.
| Uh | = Clubhead speed just before impact = 100mph = 44.7 m/s |
| Ub | = Ball speed just before impact = 0 |
| Vh | = Clubhead speed just after impact (we will compute) |
| Vb | = Ball speed just after impact (we will compute) |
| M |
= Clubhead mass = 200g = .2 Kg |
| m |
= Ball mass = 46g = .046 Kg |
| m/M |
= .046/.2 = 0.23 (Listed here because we use this ratio a lot) |
| C |
= Coefficient of restitution = .83 (max allowed by USGA/R&A) |
CASE 1 - NO ACCELERATION OF CLUBHEAD INTO BALL
This is a simple momentum transfer problem. The clubhead impacts the ball, and transfers some of its momentum to the ball. Since the clubhead is more than four times as heavy as the ball, it will still retain some considerable speed after impact -- though a lot less than before impact. The total momentum of clubhead plus ball remains the same after as it was before. And, of course, the total energy after impact will be less, because the COR is less than 1. Some energy will be lost to internal friction during the collision (mostly friction inside the ball, but a little in the clubface).We will start with the well-known general equations for a simple lossy impact.
| Vh = | C m (Ub-Uh)
+ M Uh + m Ub M+m |
| Vb = | C M (Uh-Ub)
+ M Uh + m Ub M+m |
But we know the ball starts at rest (Ub = 0), so we can simplify to:
| Vh = | M Uh - C m Uh M+m |
=
Uh |
1 -
C m/M 1 + m/M |
| Vb = | C M Uh + M Uh M+m |
=
Uh |
1 +
C 1 + m/M |
That last equation should look familiar; we use it all the time to compute ball speed.
The first equation is something we don't see as often; it gives the clubhead velocity after impact. It will be slower, because the clubhead has transferred a bunch of momentum to the ball. If we use numerical values we originally assigned for m, M, and C, the equations become:
| Vh |
=
Uh |
1
- (.83 * .23) 1 + .23 |
=
Uh * .66 |
| Vb |
=
Uh |
1 +
.83 1 + .23 |
=
Uh * 1.49 |
Again, the second equation is familiar; it is the maximum legal "smash factor" for a 200g driver head. It is generally thought of as 1.5, which is a very close rounding of 1.49.
The first says that the clubhead loses about a third of its speed in impact.
Now it's easy to solve for Vb and Vh, the ball and clubhead speeds after impact:
Vb
= 149 mph =
66.6 m/s
Vh = 66 mph = 29.5 m/s
Vh = 66 mph = 29.5 m/s
So now we know how much the head slows down, and the ball speeds up, during impact.
While we're here, let's look at the force and momentum involved.
Momentum is interesting to physicists at least in part because it relates force, time, velocity, and mass. Here's how:
Everybody know's Newton's second law: F = ma
One component of that is acceleration, which is a change of velocity over time. Physicists and mathematicians usually refer to such a change as a "delta". So a change of velocity would be "delta V" or ΔV. So:
| F
= ma = m |
ΔV t |
Or
Ft = m ΔV
The right side is the change of momentum. The left side is called "impulse", and the relationship is: Impulse equals momentum change. Physicists and mathematicians have a more general view of impulse; it does not require a constant force, as our equation does. But we prove below that, for our calculations, a constant force gives exactly the same answer as if we plotted the exact buildup and decay of force during the collision between clubhead and ball.
Let's use this, plus our results above, to compute first the momentum change for clubhead and ball, then the force the clubhead exerts on the ball to cause the momentum change:
Clubhead: mΔV = M (Uh - Vh) = .2 (44.7-29.5) = 3.0
Ball: mΔV = m Vb = .046 * 66.6 = 3.0
Good, they're the same! That means we did the arithmetic right, because the law of conservation of momentum says: any momentum gained by the ball must be lost by the clubhead. And it was.
Now for the forces. From above, impulse = momentum change:
Ft = mΔV
We know that the momentum change is 3.0 Kg-meters/sec, so:
Momentum
change = Impulse = Ft = 3.0
we also know that t = .0004, so:
.0004
F = 3.0
F = 7500 Newtons (N) = 1686 pounds
F = 7500 Newtons (N) = 1686 pounds
So the average force between clubhead and ball during impact is 1686 pounds.
CASE 2: CLUBHEAD ACCELERATES INTO BALL
In a good swing, the clubhead can accelerate into the ball by as much as 500 feet per second per second. (In MKS units, that's 152.4 meters per second per second.) The only reason clubhead acceleration might matter for distance is that there is an extra force added to the momentum transfer that we had in case 1. That force is whatever force is accelerating the clubhead. If it was accelerating the clubhead coming into impact, then it is continuing to push the clubhead during impact -- and that is where any benefit will derive.Let's use F=ma to see how much force is accelerating the clubhead just before impact:
F = ma = .2 * 152.4 = 30.5 N
=
6.85 pounds
This force will increase the momentum of the whole system during impact -- both the clubhead and the ball it is "pushing". For the .0004 seconds that the clubhead and ball are in contact, we will have an extra 7 pounds of force (we'll round 6.85 up) accelerating the whole 246-gram mass of clubhead+ball. Let's see what that does to the final velocities. (The calculations below are in MKS units.)
F t = (M + m) ΔV
| ΔV = | F t M + m |
=
|
30.5
* .0004 .200 + .046 |
=
.0496 m/s = 0.11mph |
So it has added a whole .11 mph to the combination of clubhead and ball by the time the ball separates from the clubhead. That means:
| Clubhead speed after impact | = 66 + .11 | = 66.11 mph |
| Ball speed after impact | = 149 + .11 | = 149.11 mph |
This is not much of a gain in yardage. Using the rule of thumb '1 additional mph of ball speed gives 2 additional yards', we have increased the distance by 0.22 yards, or about 8 inches.
Why is this less than the rough calculations, the simplified analyses, in the main body of the article? Because each simplified analysis was a 'back of the envelope' calculation that I could do in a couple of minutes. Any time you make a rough calculation instead of a complete analysis, you must make lots of assumptions. In each case, I had chosen an assumption to make acceleration look important. I did that because I suspected the answer would come out, "It's not that important." I didn't want my assumptions challenged as the reason it didn't look important, so the assumptions were all in favor of acceleration. Note that, even so, acceleration didn't seem all that important. But when I replaced assumptions with actual calculation, the results showed acceleration to be even less important.
DEPENDENCE ON FORCE PROFILE DURING
IMPACT
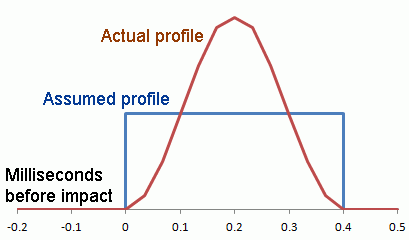One last
point: These calculations are
based on a constant force -- the
average force -- during contact between clubhead and ball. The blue force-vs-time
profile in the picture shows
this; during impact, the force is some constant value, and it is zero
all other times. Obviously
this is contrary to fact; the force starts small, increases as the ball
compresses, and decreases as the ball releases and leaves the clubface.
In other words, the red force-vs-time
profile is what is really happening.So we need to show that it doesn't matter; any force profile that gives the same average force will give the same final velocities. ("The same average force" means the same area under the profile curve.)
Below is a quick proof, in case you're interested. It involves a bit of integral calculus, but very easy and basic stuff.
The only place we make assumptions about the force profile is where we use 'impulse equals momentum change'. So let's generalize that, using F(t) for force as a function of time.
That means we re-express F t = M ΔV as F(t) dt = M dV where d means an infinitesimal delta.
To find the actual change in velocity , we need to integrate.
∫
F(t) dt = M ΔV
or, solving for ΔV:
ΔV = 1/M * ∫
F(t)dt
(Equation #1)
Equation #1 gives the change in velocity if we used the actual force profile F(t): start small, increase to a peak, then fall off again. In order to compute ΔV directly from physical principles, we would need the actual force function F(t), and then use integration to find the area under the curve.
But, in our calculations above, we used the average force over the duration of impact, Fav. Is this legitimate? Does it give the same answer?
To find out, we have to see how the average force Fav is computed? If the total time is T (in our case, 0.4 milliseconds), then the average is computed as:
Fav = 1/T * ∫
F(t)dt
In our presumably "exact" analysis, we used Fav to compute ΔV using the formula:
ΔV = Fav * T
/ M
Let's plug in for Fav the time-dependent formula for Fav using integration. So ΔV becomes:
ΔV = 1/T * ∫ F(t)dt *
T / M
ΔV = 1/M ∫ F(t)dt
ΔV = 1/M ∫ F(t)dt
That's exactly the same as Equation #1 above. Which says we get the same change in ball speed whether we use the average force or the actual force profile.
Last
modified -- January 13, 2012
|
|