 Most
instructors feel
that the folding/unfolding of the right arm (or pointing/unpointing, as
one put it recently) is an important part of the swing that the double
pendulum fails to model. Yes, it is an important part of the swing. But
the double pendulum is quite capable of modeling the important thing it
does -- add forces to the grip with the right hand. Most
instructors feel
that the folding/unfolding of the right arm (or pointing/unpointing, as
one put it recently) is an important part of the swing that the double
pendulum fails to model. Yes, it is an important part of the swing. But
the double pendulum is quite capable of modeling the important thing it
does -- add forces to the grip with the right hand.
One instructor actually insisted that I change my analysis to the model
in this picture, changing the two hinges of the double pendulum model
to six
powered hinges. Honestly!
Fortunately, the real effect of the right arm produces something the
model was designed
to handle: wrist
torque. Let's look at this in more detail.
|
The right arm and wrist
torque
 The
point of the
analysis is to compute the progress of the swing, in terms of club
position and speed. So any additional complexity due to the right arm
boils down to what the right hand does to the club. In three
dimensions, it can do six things to the club: The
point of the
analysis is to compute the progress of the swing, in terms of club
position and speed. So any additional complexity due to the right arm
boils down to what the right hand does to the club. In three
dimensions, it can do six things to the club:
- Force in the swing plane -- the red arrow in the
picture.
- Torque in the swing plane -- the circular blue arrow
in the picture.
- Force perpendicular to the swing plane. (If we could
show it, it would be towards or away from the viewer of the picture.)
- Torque perpendicular to the swing plane.
- Axial force -- force along the axis of the shaft.
- Axial torque -- rotation of the club around the axis
of the shaft.
All of these forces can theoretically be exerted by the right hand on
the grip of the club.
But let's remember what a double pendulum model
is used for. It computes the progress of the swing, in the swing plane.
It is a two-dimensional analysis.
- Motion of the club (or golfer)
perpendicular to the swing plane is not interesting to the analysis,
nor is axial rotation of the club. Both are very interesting to the
direction the ball will travel, but you'll never see a double-pendulum
analysis that deals with clubface direction, except for wrist cupping
or bowing that adds or subtracts loft at impact. Most issues of
clubface direction and clubhead path require a totally different
approach to analysis.
- As for axial force, it turns out to be the way
shoulder torque is conveyed to the club. It has already been accounted
for in the shoulder torque.
|
 So,
from the entire list above, only #1 and #2 (in-plane force and torque)
are relevant to a double pendulum model's job. It is easy to see how
the in-plane torque is accounted for; it is simply part of the wrist
torque. But we still don't see
where a double pendulum is able to account for the force. So,
from the entire list above, only #1 and #2 (in-plane force and torque)
are relevant to a double pendulum model's job. It is easy to see how
the in-plane torque is accounted for; it is simply part of the wrist
torque. But we still don't see
where a double pendulum is able to account for the force.
This picture shows that the model can also handle
the in-plane force. Any force exerted by the right arm in-plane is a
push or a pull on the grip. (The picture shows a push.) That force
works against the pull or push of the left arm. In other words, the
left hand
acts as a fulcrum or pivot, and the right hand's force tries to turn
the club around this pivot.
But what is such a turning force? It
is a torque. And how big is it? It is the size of the force,
times the
distance between the force and the fulcrum. So any action of the right
arm can be factored into a double pendulum model as wrist torque,
because either it is a torque (the blue arrow above) or it can be
computed as one (the red arrow above).
|
Here's
a bonus observation:
- If your favorite swing uses this sort of positive wrist torque to cause clubhead release, for either
control or power, then a ten-finger grip (or baseball
grip) is appropriate. That's because you increase the distance between
force and fulcrum, thus increasing the wrist torque.
- If,
on the other hand, you believe the "standard swing" model is right for
you (with no wrist torque), then an overlap grip is preferable. The
less distance between the hands, the less opportunity for unwanted hand
action to produce wrist torque. In fact, some good players (Jim Furyk
comes to mind) use a double-overlap grip, which further reduces the
torque-multiplying separation between force and fulcrum.
|
 But
the picture above is not the only way the arms can work to produce
wrist torque. The opposite sense is also feasible. Suppose the right
arm is pulling and the left is pushing. That creates a "negative
torque", a torque that tends to prevent the club from releasing. It
will encourage holding and perhaps even increasing the clubhead lag. But
the picture above is not the only way the arms can work to produce
wrist torque. The opposite sense is also feasible. Suppose the right
arm is pulling and the left is pushing. That creates a "negative
torque", a torque that tends to prevent the club from releasing. It
will encourage holding and perhaps even increasing the clubhead lag.
This is not mere speculation. Kelvin Miyahira has been looking at lag
from a biomechanics viewpoint rather than the physics approach I am
comfortable with. By studying videos of golfers (including a lot of Tour players),
he has identified a number of "micro-moves" that encourage the
retention of clubhead lag. Two of the important micro-moves are left
arm extension and a right elbow tucked down in front of the body
through almost the entire downswing. That is exactly the diagram we
show here:
- The extended left arm is a pushing force at the butt of the grip.
- Tucking the right elbow prevents it from extending,
"shortening" the right arm. Do this assertively and not just passively,
and the right hand is pulling the grip.
The net result is a negative torque, one that prevents the release of
the lag until inertial forces are irresistible in releasing the
clubhead. Kelvin's observation is consistent with physics theory in
this regard.
|
The right arm and
shoulder torque
 For a long time, I
didn't think the right arm could affect shoulder torque. But some
recent analysis suggests that it can. No, it doesn't actually affect
the shoulder torque itself. But you can model certain
right arm actions as a change in shoulder torque. And, since the double
pendulum is not reality but rather a model useful for analysis, that is
as relevant as anything could possibly be. For a long time, I
didn't think the right arm could affect shoulder torque. But some
recent analysis suggests that it can. No, it doesn't actually affect
the shoulder torque itself. But you can model certain
right arm actions as a change in shoulder torque. And, since the double
pendulum is not reality but rather a model useful for analysis, that is
as relevant as anything could possibly be.
The diagram at the right is a re-drawing of the double-pendulum model.
The important thing here is that the length of the inner member of the
pendulum (representing the arms) defines a circular arc of radius R,
and the hands move along that arc as if they were on a track. They are
driven around that track by the shoulder torque. Expressed
more accurately... |
 They
are driven around the track by a force due to the shoulder torque,
shown in the diagram to the left. Since the path is a perfect circle,
the magnitude of the force is They
are driven around the track by a force due to the shoulder torque,
shown in the diagram to the left. Since the path is a perfect circle,
the magnitude of the force is
Force = ShoulderTorque / R
and the force acts exactly tangent to the arc.
Anybody familiar with physical modeling can see immediately that both
pictures of the model -- the double pendulum and a circular track for
the hands -- gives an identical result for any analysis. So, even
though it looks different and the equations you get might look
different, the answers will come out the same. Anyplace you could use a
double pendulum analysis, you could use a curved-track analysis.
Why
is this even interesting? Because one of the criticism's
leveled against the double pendulum model that the path of the hands is
not circular. Due to the folding of the right arm, the radius may be
shorter at the top of the backswing. (May be.
But not "must be". It depends upon which muscles transfer the shoulder
torque to the hands, which is an issue of swing keys and technique.)
Does this invalidate the model? Probably not. For years, it has given
realistic, accurate results when modeling the swings of real golfers. Cochran
& Stobbs noticed this as early as 1968. Jorgensen
quantified it in the mid-1990s. Other researchers have been similarly
successful using it to model the real golf swing.
|
But
sometimes it is necessary to take into account the folding of the
right arm. When that happens, the circular track becomes a useful
modeling tool, more useful than the original pendulum representation.
If the path does not vary too radically from a circular curve, you can
use the diagram below to represent the hands as a carriage moving along
a track.
 In the diagram: In the diagram:
- The dotted line shows the direction of the center of
rotation (the shoulder pivot). The center is a radius r
from the hands. (The radius is lower-case this time, to indicate that
it varies over the course of the swing.)
- The black dashed line is the actual path of the
hands. The important thing to notice here is that it is not a circle
around the shoulder pivot; if it were, then it would be perpendicular
to the dotted-line radius. So there is some angle between the actual
path and an ideal circular path.
- Shoulder torque produces a force along the ideal
circular path; that is what torque does. The force is shown in blue,
and is of a magnitude equal to the torque divided by r.
- The force can be resolved into components, shown in
aqua. One component (the bold one) is parallel to the path of the
hands, and so accelerates the hands along their path. The other (the
very pale one) does nothing to aid or hinder the progress of the hands,
and is rather small as well; we can ignore it for most analysis
purposes.
How is this diagram useful for analysis purposes? It tells us that we
can get a rather good approximation of reality by using the double
pendulum model and tweaking the shoulder torque profile (that is,
shoulder torque vs time) to provide the actual accelerating force that
the hands see.
 How
can we use this to analyze non-circular swings? From
photographs
or slow-motion measurements of the swing, plot the path of the hands as
it varies during the downswing. The key piece of information needed is r(t)
, the distance from the path to the center of rotation, as it varies
over time. Using r(t),
calculate the shoulder torque as a function of
time that would give the same accelerating force Fa
if the model were a conventional double pendulum of fixed radius R.
Then just run the double-pendulum model using the newly calculated
shoulder torque, and you will get a behavior that mirrors the
non-circular swing, especially in the vicinity of impact. How
can we use this to analyze non-circular swings? From
photographs
or slow-motion measurements of the swing, plot the path of the hands as
it varies during the downswing. The key piece of information needed is r(t)
, the distance from the path to the center of rotation, as it varies
over time. Using r(t),
calculate the shoulder torque as a function of
time that would give the same accelerating force Fa
if the model were a conventional double pendulum of fixed radius R.
Then just run the double-pendulum model using the newly calculated
shoulder torque, and you will get a behavior that mirrors the
non-circular swing, especially in the vicinity of impact.
Actually, that is an oversimplification. It would work if all the mass
of the arms, hands, and club were accelerating linearly, so we could
apply simple F=ma.
Since it is rotating, we have to calculate the varying moment
of
inertia of the arms, hands, and club as r(t)
varies. That sounds
complicated, but it isn't bad at all in practice. The diagram changes
to the one at the left, stressing moment of inertia instead of forces.
If you are interested
in more detail of the altered model, including an example of its use,
you can get it in my article on the right-side swing.
|
 But
there is a constraint on where you can use this modification of the
model. The "strobe" diagram on the right is adapted from the SwingPerfect
computer program. The circular path of the hands is clearly apparent as
the collection of green and red dots, representing the hands at each
"snapshot". I have modified SwingPerfect's diagram to color-code the
dots: green while the initial wrist-cock angle is still intact, and red
once the club swings out and releases the wrist cock. As long
as the wrist cock angle is not changing (green dots),
our modeling is quite good. But, once centrifugal force starts to
release the clubhead (red
dots), accuracy depends on the hands being on the circular
path. There are a few reasons: But
there is a constraint on where you can use this modification of the
model. The "strobe" diagram on the right is adapted from the SwingPerfect
computer program. The circular path of the hands is clearly apparent as
the collection of green and red dots, representing the hands at each
"snapshot". I have modified SwingPerfect's diagram to color-code the
dots: green while the initial wrist-cock angle is still intact, and red
once the club swings out and releases the wrist cock. As long
as the wrist cock angle is not changing (green dots),
our modeling is quite good. But, once centrifugal force starts to
release the clubhead (red
dots), accuracy depends on the hands being on the circular
path. There are a few reasons:
- The double-pendulum model reflects that most of the
clubhead speed is due to the release of the wrist cock transferring
energy from the hands and arms to the clubhead. How much energy is
transferred depends on the curvature of the path of the hands during
the release. If we change the path of the hands, we will get a
different clubhead speed. So the path of the hands once the wrist angle starts
increaing must be the circular path being calculated by
the model.
- During release (once the wrist angle starts
increasing), tension in club's shaft is exerting a force on the hands
that slows them down. Notice that means the force is one that opposes
the shoulder torque, which is accelerating the hands. But opposing
shoulder torque is what moment of inertia does. So, since we are
varying the model by playing with moment of inertia, our formula for
MOI would need to get a lot more complicated during release in order to reflect this force. Better we
get to the circular path before release, so we can use the proper
double-pendulum model and a relatively simple formula for moment of
inertia.
So we have a condition for the altered
model to work: By
the time the wrist cock reduces significantly from its original angle,
the hands must have reached the circular path assumed by the model.
That is true for many interesting variants of the
swing. In fact, the so-called "standard swing", where there is no wrist
torque applied except to keep the club from falling in to the center of
the swing, has essentially no change in wrist cock angle for about 60%
of the downswing time. |

 The
double-pendulum model is the basis for every
physical analysis and
simulation of the golf swing that I have seen. It holds that
the moving parts of the swing are an inner member (green)
representing the arms and shoulders, and an outer member (black) representing
the club.
The
double-pendulum model is the basis for every
physical analysis and
simulation of the golf swing that I have seen. It holds that
the moving parts of the swing are an inner member (green)
representing the arms and shoulders, and an outer member (black) representing
the club.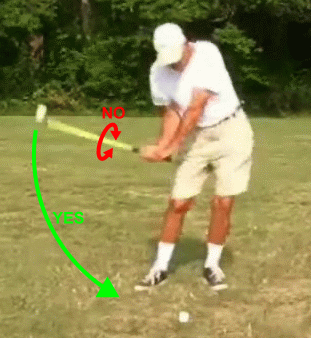
 There
are
certainly many
variations using this model. For instance, the "standard swing" applies
a positive wrist torque early in the downswing, for the purpose of
keeping the wrist cock angle from falling into the middle of the swing.
This torque is usually represented by a "stop" that holds the wrist
cock angle; but it is really a torque that peaks very early and drops
to zero about a tenth of a second into the downswing. By that time,
centrifugal force on the club is more than enough to keep the wrist
cock angle from shrinking; in fact, the club wants to fly out -- to
release. So no further wrist torque is needed for the stop.
There
are
certainly many
variations using this model. For instance, the "standard swing" applies
a positive wrist torque early in the downswing, for the purpose of
keeping the wrist cock angle from falling into the middle of the swing.
This torque is usually represented by a "stop" that holds the wrist
cock angle; but it is really a torque that peaks very early and drops
to zero about a tenth of a second into the downswing. By that time,
centrifugal force on the club is more than enough to keep the wrist
cock angle from shrinking; in fact, the club wants to fly out -- to
release. So no further wrist torque is needed for the stop. Most
instructors feel
that the folding/unfolding of the right arm (or pointing/unpointing, as
one put it recently) is an important part of the swing that the double
pendulum fails to model. Yes, it is an important part of the swing. But
the double pendulum is quite capable of modeling the important thing it
does -- add forces to the grip with the right hand.
Most
instructors feel
that the folding/unfolding of the right arm (or pointing/unpointing, as
one put it recently) is an important part of the swing that the double
pendulum fails to model. Yes, it is an important part of the swing. But
the double pendulum is quite capable of modeling the important thing it
does -- add forces to the grip with the right hand. The
point of the
analysis is to compute the progress of the swing, in terms of club
position and speed. So any additional complexity due to the right arm
boils down to what the right hand does to the club. In three
dimensions, it can do six things to the club:
The
point of the
analysis is to compute the progress of the swing, in terms of club
position and speed. So any additional complexity due to the right arm
boils down to what the right hand does to the club. In three
dimensions, it can do six things to the club: So,
from the entire list above, only #1 and #2 (in-plane force and torque)
are relevant to a double pendulum model's job. It is easy to see how
the in-plane torque is accounted for; it is simply part of the wrist
torque. But we still don't see
where a double pendulum is able to account for the force.
So,
from the entire list above, only #1 and #2 (in-plane force and torque)
are relevant to a double pendulum model's job. It is easy to see how
the in-plane torque is accounted for; it is simply part of the wrist
torque. But we still don't see
where a double pendulum is able to account for the force. But
the picture above is not the only way the arms can work to produce
wrist torque. The opposite sense is also feasible. Suppose the right
arm is pulling and the left is pushing. That creates a "negative
torque", a torque that tends to prevent the club from releasing. It
will encourage holding and perhaps even increasing the clubhead lag.
But
the picture above is not the only way the arms can work to produce
wrist torque. The opposite sense is also feasible. Suppose the right
arm is pulling and the left is pushing. That creates a "negative
torque", a torque that tends to prevent the club from releasing. It
will encourage holding and perhaps even increasing the clubhead lag. For a long time, I
didn't think the right arm could affect shoulder torque. But some
recent analysis suggests that it can. No, it doesn't actually affect
the shoulder torque itself. But you
For a long time, I
didn't think the right arm could affect shoulder torque. But some
recent analysis suggests that it can. No, it doesn't actually affect
the shoulder torque itself. But you  They
are driven around the track by a force due to the shoulder torque,
shown in the diagram to the left. Since the path is a perfect circle,
the magnitude of the force is
They
are driven around the track by a force due to the shoulder torque,
shown in the diagram to the left. Since the path is a perfect circle,
the magnitude of the force is In the diagram:
In the diagram: How
can we use this to analyze non-circular swings?
How
can we use this to analyze non-circular swings? But
there is a constraint on where you can use this modification of the
model. The "strobe" diagram on the right is adapted from the
But
there is a constraint on where you can use this modification of the
model. The "strobe" diagram on the right is adapted from the