Home ⇒ golf ⇒ swing ⇒ Current Article

Nesbit or Kwon or MacKenzie?

Dave Tutelman -- December 5, 2018

Shaft bend - a deeper look

If you read the article I originally posted in October 2018 and just want to know what is new in this version, I have a summary of the new insights here.

Let's bring in another Nesbit paper. In 2010, Nesbit and Ryan S. McGinnis published an analytical study of shaft bend during the downswing. See McGinnis and Nesbit, "Golf Club Deflection Characteristics as a Function of the Swing Hub Path", The Open Sports Sciences Journal, 2010, 3, 155-164. Manzella and Jacobs point to it as proof that their model "has it covered" when I talk about shaft deflection being a "meter needle" for hand couple.

Let's review that paper here, to see if we can find a reason for the difference between Nesbit and most other biomechanists in the hand couple issue. We'll do it at a high level, with the hope that everybody will be able to get it. I have also included an appendix, where I'll discuss the math for those who want to see a little more of the technical detail. (I'm not doing a complete analysis there by any means, just going into some of the equations to show my reasoning.)

Nesbit's bottom line: curvature at impact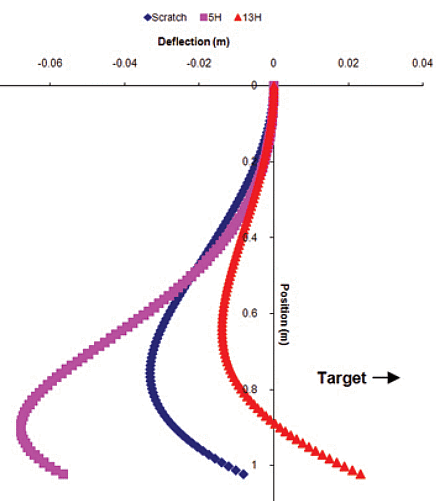

Let's cut right to the shaft shape at impact. The figure, directly from their paper, shows the shaft deflection (horizontal axis) vs position along the shaft (vertical axis). The three curves are the shaft shapes for the same three male golfers as in their other studies (like Work and Power). The horizontal axis is enlarged by a factor of ten, so the bend is much exaggerated. I see two very interesting and surprising things about the result:

Only the 13 handicap, the worst golfer in the study, had the shaft tip in lead at impact. The two better golfers had a net lag bend. In fact, the 5 handicap has 6cm -- more than 2.3 inches -- of lag deflection.
The shaft itself has a double curve. The shaft has lag curvature near the hands and a pronounced lead curvature near the clubhead.

Both results are contrary to experience of clubfitters, shaft manufacturers, and shaft researchers.

Everybody with shaft experience can tell you that the curvature makes the tip lead at impact. (I intend that to mean that, if you extend the centerline of the shaft at the hands, the tip is to the target side of that line. It certainly seems to agree with Nesbit's meaning, based on this graph and the equations from which he derived it.)

At least as interesting is the reverse curvature near the hands for all three of the golfers. We know that, contrary to the graph, the shaft curvature less than .2m below the mid-hand point is lead curvature. How do we know this? That is where the TrueTemper ShaftLab strain gauges are placed, and they measure curvature directly at that point. Since they always report lead curvature at impact for every swing I have seen or heard of, the curvature at .2m should be lead curvature in order to agree with experimental data. But Nesbit's result isn't, not for any of the curves in the graph.

Just a few technical details. Feel free to skip them.

My comments assume that zero on the vertical axis is the mid-hands point. That appears consistent with the shaft's length of just over 1m for the driver. It would be 1.17m if zero on the axis were the butt of the shaft.

Brief point of explanation about ShaftLab output. They report lead/lag as inches at the tip, based on an assumed model of curvature along the length of the shaft. This assumption is not a double-curve, so I would not use ShaftLab to argue about where the tip is. But their curvature model is pretty simple; if the curvature is lead at the strain gauges, then they report a lead deflection at the tip consistent with the curvature at the strain gauge. Similarly for lag curvature. So looking at their report of tip deflection gives us a directly proportional measurement of curvature at the strain gauges. If you didn't understand that point, don't worry too much about it. If you understood and disagreed, I'd like to hear about it.

Why does Nesbit's model give results so much at odds with experience? To answer that, we have to start by looking at the model's assumptions and their consequences.

A few key assumptions

Here are three assumptions built into the Nesbit model from the beginning. Two can be shown to be wrong, and the third is questionable at best. Let's quote then examine each of them.

(1) All damping of the shaft's vibration is due to friction within the shaft
From the paper:

In order for a reasonable solution to be attained, a damping term needs to be added to the deflection equation so that the final equation is of the form displayed in Equation 2. The damping term represents the natural damping that is provided by the shaft material and the hands of the golfer.

The words "damping that is provided by the shaft material and the hands of the golfer" are very true. But this statement is not followed through into the analysis. The equations of motion (equations (2) through (8) in the paper) only show damping from the shaft material, none from the hands. Yet a simple experiment can show us that, hard as it is to quantify theoretically, the real-life damping is dominated by the hands, not the shaft material.

Here is a video showing that experiment. In the video, we try three possible models of damping.

Model	Description of securing the butt	Description of damping behavior
Clamped	The pure cantilever model, with the butt firmly clamped against any motion. The demonstration here is almost as good as the clamp of a frequency meter.	The response is almost undamped. The oscillations lose only about 2.5% of amplitude each cycle.
Hands	A perfectly normal golf grip. I tried to keep my hands as still as I could, but it can't be done. The hands cannot adapt the applied torque quickly nor responsively enough to the vibrating shaft.	The response damps out very fast. There is a little overshoot, but damping is essentially complete during the first cycle.
Braced	In between "clamped" and "hands". The fingers are resting tightly against a rigid surface, so the only damping comes from the palm and finger pads on the handle of the club.	The response is in between as well. There is considerable damping, but not before a few cycles are completed. In this example, it was four cycles, but has varied from two to four. Four is sort of a maximum encountered. I would estimate an amplitude loss of about 70% each cycle.

The Nesbit assumption as stated in words includes both the shaft and the hands. But the equations in the model include only internal shaft friction, which is the "Clamped" model. If this were an accurate picture, there would be a lot of ringing vibration in every swing.

When the golfer makes a swing, it is clear that the club is being held in the hands, not clamped. I believe the most accurate model is "Hands", because there is nothing to brace the hands during the swing, as the club yanks the hands around late in the downswing. But one could make the argument that the torques moving the hands -- which in turn move the handle of the club -- are calculated in the model and should not be relegated to just a damping role. That would call for something closer to the "Braced" model. If you do adopt the "Braced" model, you need to be sure it includes (a) the hands' being torqued by the club and not just vice versa, as well as (b) biomechanical constraints on the hands' ability to track that torque while holding the club steady. I don't recall ever seeing such a model, but it might well be there.

Either way, "Hands" or "Braced", there is an order of magnitude more damping from the hands than there is in the shaft itself. So Nesbit's "Clamped" analysis greatly underestimates the damping.

(2) All shaft bend near impact is due to eccentric centrifugal loading
From the paper:

Assuming that, when compared to the normal force, tangential force and torque are virtually negligible during this period, it is logical that a large normal force would result in a significant reduction in club head deflection. This behavior is due to the offset of the center of mass of the club head behind the centerline of the shaft. This geometry will produce a resultant moment that acts on the club head in response to a large normal force applied to the grip. This moment will work to negate any deflection in the club head while producing the shaft shape that we see at impact.

First off, what does this even mean? It means that centrifugal force on the clubhead occurs through the center of gravity of the clubhead, which is not on the shaft axis.

The picture at the right shows what happens when the pull is eccentric, meaning off-center or not on the shaft's axis. I have substituted an easy-bending aluminum yardstick for the shaft, and a long bolt for the part of the clubhead between the shaft axis and the CG. The pulling force is a shoelace wrapped around the bolt just below the head. When I pull on the shoelace, it bends the "shaft" as shown. (I have exaggerated the curve by the angle of the photo, but I haven't distorted it, at least not in the sense of creating bend from nothing.) The reason for the bend, in intuitive terms, is that the force wants to line up with the "hands" that are holding the other end of the shaft.

The reason in terms of physics is that the force is not in line with where the bolt meets the yardstick. There is a distance between them labeled the "moment arm". The force time the moment arm creates a moment, a torque, applied by the bolt to the shaft. That moment bends the shaft.

Nesbit's paper says that, by the time of impact, all the force is centrifugal (normal, or perpendicular, to the head's velocity) and only a negligible amount is tangential (still accelerating the clubhead along its arc). So the shaft shape at impact is due only to this centrifugal eccentric loading.

There is no doubt that knowledgeable golf engineers have agreed with this assumption in the past. Wishon has said so, as have Werner & Greig. But today we have both experimental evidence and mathematical modeling showing this is not true.

The experimental data comes from TrueTemper's ShaftLab. The data was taken of tour players' swings before 1998, because I got the data from ShaftLab's instruction manual in 1998. It shows that the forward bend of the shaft is more than would be expected from eccentric loading alone.

This pair of graphs plots the toe droop and lead curvature in inches for the sample golfers' swings. The line labeled CG is drawn at the angle the center of gravity is from the shaft axis. If all the shaft bend were due solely to the eccentric loading of the shaft by the CG, then all the dots would have been on the line labeled CG, because both toe droop and lead bend would be caused by the same mechanism. Instead, the lead is more than would be predicted by eccentric loading alone, in every case. In fact, most of the data points (all but two 5-iron shots) show the lead deflection to be more than twice what the CG line would have us believe. So not only is there something more than eccentric loading at work, that "something more" is stronger than eccentric loading.

That is the experimental data. But we also have a mathematical model that gives the same result. In March 2009 in Sports Engineering, MacKenzie and Sprigings published a paper entitled "Understanding the mechanisms of shaft deflection in the golf swing." In order to test the assertion of shaft bend due to eccentric loading ("axial force" in their paper), they ran the model with three different clubheads:

Normal - the normal position of the center of gravity.
In-line - the center of gravity in line with the shaft axis, so there is no eccentric loading.
Reversed - The center of gravity moved exactly opposite the normal position; that is, forward and heelward of the shaft.

Here is how the deflections looked for each case. The left graph is toe-up-down deflection and the right is lead-lag.

The toe droop looked the way you would expect. The normal case had down-droop, the reverse case was toe-up, and the in-line case was just about zero deflection. That tells us that toe droop is indeed due to eccentric centrifugal loading.

But the lead-lag deflection was completely different! All three clubs, even the reverse-CG club, had lead deflection at impact. That means that there is a mechanism at work causing lead deflection. Moreover, this mechanism is even stronger than eccentric loading, because even the reverse-CG case had lead deflection. That's the same thing we saw in the experimental data; the other mechanism is stronger than eccentric loading.

So there you are! Both experimental data and an analytical model that show the lead/lag deflection at impact is more than just eccentric loading due to centrifugal pull; indeed, the other effect is at least as strong and likely stronger.

(3) A cantilever beam
From the paper:

I made the choice to represent the grip side as a cantilever beam , because very little is known about the interactions between the golfer’s hands and the club and this assumption makes the equations of motion easier to solve.

Easier to solve, for sure. But this assumption has a few problems.

We've already seen the problems in the "damping" section, because they also have consequences there.

It implies a rigid clamp, not easily modeled by hands that provide the lion's share of the damping.
It implies that the hands torque the club and thus control its motion, but the reverse is not true; the club cannot torque the hands and move them. We know this is contrary to fact.

Rather than saying anything more about the cantilever assumption here, we will hold off for a few subsections.

Transient analysis

If everything were perfectly static -- the shaft had reached steady state, with no changing forces or torques on it -- then we would expect a single curve, not the double curve in Nesbit and McGinnis. But, because the shaft itself weighs something, it takes a little time for the entire length of the shaft to reach its steady-state deflection. Their paper is about characterizing how the shaft bend during the golf swing differs from what a static analysis would be, given the same torques and forces in steady state. That is an excellent question to ask! Let's see if it should give a double bend at impact.

Nesbit and McGinnis talk about "bending modes" in the paper. Bending modes implies a resonant effect leading to standing waves. Strong damping at the handle suggests this is not the best way to think about the transient behavior. Instead, let's show how a shaft would behave under dynamic load.

Here is a diagram I think that both Nesbit and I could agree to, at least with the explanation here:

For the early part of the downswing, the shaft bend is completely in lag, because the hand couple is needed to get the club moving and turning.
At some point, about 100msec before impact, there is a force pulling the head forward along its path. This curves the shaft forward, but initially just at the tip. Because of shaft mass, this "flex wave" has yet to reach the hands. It must propagate up the shaft to the hands. Until it reaches the hands, the curve at the grip remains in lag bend.
If the force continues to pull the head forward, eventually, the shaft will be completely in lead bend. According to McGinnis and Nesbit's analysis, impact occurs before the flex wave reaches the hands, so there is still lag bend under the hands at impact.

Without having talked about bending modes, we have a nutshell description of why the shaft might be shaped as Nesbit says. Accepting that shape requires accepting at least one of two things:

The propagation is slow enough so the flex wave has not reached the hands by impact, or the flex wave bounces up and down the shaft, so it is still active -- bending the shaft backwards at the hands -- when impact occurs.
The force pulling the head forward goes away before impact.

We can dispose of the second pretty easily. The second assumption I flagged is that eccentric loading is the only force bending the shaft at impact. We know there must still be something pulling the clubhead forward relative to the shaft, because both experiment and analysis says there is more lead bend than we could get from just eccentric loading. In fact, this mechanism provides more of the bend at impact than we get from eccentric loading.

So what about the propagation of the flex wave. First, let's look at the speed of the wave. A flex wave can be seen pretty dramatically in the video at the right. The wave is started by the sudden disturbance of the tip caused by impact. The movie was taken by Russ Ryden in 2009 at 1200 frames per second. The wave created by impact is a sudden acceleration at the tip of the shaft in a lag direction. That sudden lag is imposed on an overall lead bend. (The high shutter speed assures that very little of this bend is rolling shutter distortion.)

It is easy to see in the video that the reversal of the shaft bend travels up the shaft to the grip over the course of a few frames, and the shaft more or less "settles" into this new shape. Looking closely at still frames of Russ' video, I conclude that the wave travels the length of the shaft, clubhead to hands, in about 3 milliseconds.

No matter what the shape or amplitude of the flex wave, it travels along the shaft at the same speed. So a more gradual change in deflection at the tip, such as the one in the picture above showing the lead bend propagating up the shaft, would also travel the length of the shaft in 3 milliseconds. When the wave reaches the grip, one of three things happens:

If the shaft is accurately modeled as a clamped cantilever, the wave bounces back down the shaft.
If the handle and hands damp everything on the first cycle, the wave is absorbed and vanishes.
If the handle and hands damp some but not all of the wave, some portion of the wave propagates back down the shaft.

We should recognize these three cases as "clamped", "hands", and "braced" respectively from our previous discussion.

Any portion of the wave reflected from the handle down the shaft will be reflected at the tip intact; the clubhead is fastened to the shaft rigidly, at least as compared with any model of the handle and hands. So, grip end, here it comes again! The absorption or reflection happens in the same way it did the first time. And the cycle repeats until the wave is too weak to make any difference.

Let's see what this means for the cases above:

Clamped: The wave could be bouncing back and forth for a while. It might even produce a standing wave. But we really don't need to worry about this one. The rigid clamp model of the golfer's hands has little relation to reality.
Hands: There is almost 100% absorption of the wave, so the wave travels once up the shaft and disappears. It has a practical presence for only 3 milliseconds.
Braced: The wave is absorbed about 70%. By the third or fourth time up the shaft, we can ignore it. Since a round trip is 3msec twice (once down and once up) or 6 msec, this means that the transient wave will be negligible in about 20 milliseconds. (In my opinion, the number will be closer to 3, but let's leave 20 as a possibility.)

This transient analysis tells us that any transient -- any difference between the instantaneous and the steady-state shape of the shaft -- will be gone 3 to 20 milliseconds after the tip force that caused it. So we can expect the entire shaft to be in lead bend less than 20 msec after the tip is pulled into lead bend, and probably closer to 3 msec.

But the pull on the clubhead starts 100 msec before impact, and most sources have some lead curvature of the shaft at least 30 msec before impact. So consider:

At least 30msec before impact, the forces and torques at the tip of the shaft create lead curvature there.
It takes 3-20 msec (probably closer to 3) for a transient to die out.

The inevitable conclusion is that the entire shaft must be in lead curvature by impact. So transients are not going to give the shaft shape at impact that Nesbit's analysis shows.

Static analysis

"Inevitable conclusion"? Well, maybe not quite inevitable. At least not if you buy Nesbit's assumptions, specifically:

Eccentric loading accounts for all bending at impact.
The shaft acts as a cantilever beam.

The first has been shown untrue, and the other is questionable at best. But let's see what happens -- even statically -- if they are both true.

This may seems like a digression, but bear with me. In 2014, I had a conference call with Sasho MacKenzie and Russ Ryden. We were talking about a bunch of shaft behavior issues, and I had a question prepared for the meeting. I wanted a model of eccentric loading, and had sent both of them this picture.

You will recognize the third (the right-hand) photo as the one I used earlier to illustrate what eccentric-load bending is. The first is just to convey that the ruler was pretty straight to begin with; there is no warped ruler giving us incorrect messages about bending. The second (middle) photo shows what happens if you clamp the butt of the shaft before pulling -- applying the eccentric load.

My question was: which do we think is a better model for hand action, #2 (clamped) or #3 (hinged). We all agreed pretty quickly that hinged is much closer to the way a real golfer holds the club. If you perform your own damping test as in my video, you will experience how much effort it takes to hold the shaft pointing in a particular direction. And that's when it's all you have to focus on; if you're trying to hit a golf ball over a water hazard to a green your focus will be elsewhere. So the "clamped" picture was a non-starter in our discussion.

But, putting that aside, suppose the correct answer were "butt clamped". Doesn't that picture look a little different? Maybe as if it has a little lag curvature near the clamp? (That is, the opposite curve of most of the shaft.)

Let's take a good look at the middle picture; how would we characterize its shape? First, let's stretch our horizontal axis the way Nesbit does in his paper, to show the curve better. We can see that in the picture on the right. Now the ruler/shaft bends sharply in lag near the clamp, before changing to lead for most of its length.

That looks a little more like Nesbit's shaft shape at impact. And we don't have to think about higher mode vibrations or transient response of the shaft. This is purely a static phenomenon.

We can even explain why the lag bend at the clamp is so sharp and so short compared with Nesbit's graph. My photo is a demonstration with a ruler, which has a single flexibility (the same EI) for its entire length. Nesbit's analysis is of a real golf shaft, which is stiffer at the butt than the tip. He shows the EI curve of his shaft in his Figure 7, and the EI near the clamp is almost four times that at the tip. So the lag curve at the clamp will show nearly four times the radius of curvature that the ruler would. That will necessarily make the lag curve longer and not as sharp.

While we are at it, this also explains the positive couple at impact that Nesbit reports. This is completely consistent with my assertion that shaft bend is a "meter needle" for hand couple. It takes a positive couple to hold the shaft in lag bend, as here where the hands are acting as a clamp.

Summary

There is a distinct difference between the couple reported by Nesbit and that of other biomechanists. Nesbit is the only one who thinks that a positive couple coming into impact is a fairly normal occurrence.
There is no terminology gap to explain the difference. It is a real difference in result.
I believe that the couple at impact is negative in all but pathological swings (if at all). The primary reasons for this belief are:

The forces on the handle have been measured directly by an instrumented golf club.
Shaft bend is a good indicator for hand couple, and that has also been measured directly.

Nesbit's own analysis of shaft bend may hold the clue to the differences. In particular, some questionable assumptions in his analysis are capable of providing both the reverse bend under the hands and the positive hand couple at impact.
Reading between the lines of Nesbit's comments in "Work and Power", the best golfer in his study had negative couple at impact. It would appear we don't want to teach positive couple as a good thing.

Let me repeat my desire to see Dr. Nesbit join the discussion -- but I'm not holding my breath.

Last modified -- Dec 21, 2018